On montre que dans une trajectoire elliptique, l’énergie mécanique Em du satellite ne dépend que du demi-grand axe de l’ellipse et s’exprime par la formule :
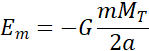
L’énergie mécanique du satellite est la somme de son énergie cinétique et de son énergie potentielle. Ainsi :
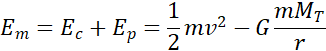
En égalant les deux expressions de l’énergie mécanique, il vient après simplification :
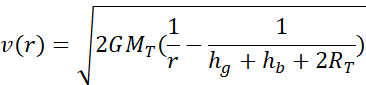
Au point A (au périgée), on a r = RT + hb et au point B, r = RT + hg. L’application numérique donne vpérigée ≈ 10,24 km.s-1 et vaphélie ≈ 1,60 km.s-1.
Nous venons de calculer les vitesses du satellite au périgée et à l’apogée de son orbite de transfert elliptique. Pour déterminer les accroissements de vitesse qu’il convient de lui communiquer lors de ses changements d’orbite, il nous reste à calculer ses vitesses aux points A et B sur des orbites circulaires. Pour ceci, il nous suffit d’égaler la force centrifuge et la force gravitationnelle s’appliquant sur le satellite le long de son orbite circulaire.
En écrivant de manière générale que, sur un cercle de rayon d décrit autour de la Terre, on a la relation :
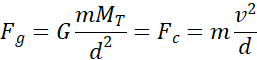
On isole v, ce qui donne :
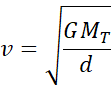
En A (c’est-à-dire avec d = RT + hb), v ≈ 7,78 km.s-1.
En B (c’est-à-dire avec d = RT + hg), v ≈ 3,07 km.s-1.