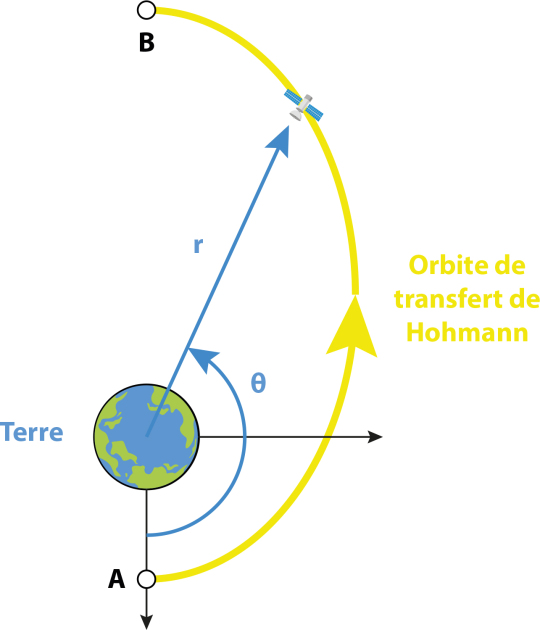
Son demi-grand axe a vaut a = ½ (hg + RT + hb + RT) = ½ (hg + hb + 2RT).
Dans le repère défini par le foyer F, occupé par la Terre et l'axe focal, l'équation polaire de l'ellipse est :
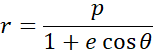
où p et e sont le paramètre et l’excentricité de l’ellipse.
Évaluons cette expression en A, où r = RT + hb et θ = 0. Il vient :
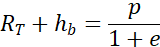
Évaluons maintenant cette expression en B, où r = RT + hg et θ = π. Il vient :
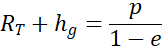
La rapport membre à membre de ces deux expressions donne, après simplification :
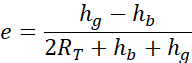
Nous connaissons a et e, nous pouvons en déduire le demi-petit axe b à l’aide de la formule :
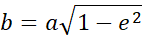
L’ellipse est maintenant caractérisée. Passons aux applications numériques.
hb est donné par l’énoncé et vaut 200 km. Le rayon équatorial de la Terre s’élève à 6 378 km.
Il nous reste à calculer hb, c’est-à-dire l’altitude de l’orbite géostationnaire.
Notre petit satellite de masse m, en orbite circulaire de rayon hg + RT autour de la Terre (de masse MT), est soumis à une force d’origine gravitationnelle dont la norme Fg est :
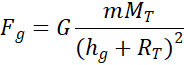
où G est la constante gravitationnelle (≈ 6,67.10-11 m3kg-1s-2).
Dans un repère lié au satellite, celui-ci subit une force centrifuge de norme Fc :
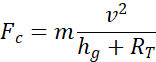
où v est sa vitesse qui, sur une orbite circulaire décrite avec une période T, vaut :
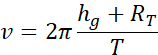
De l’égalité Fg = Fc, on déduit après simplification :
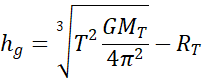
Avec T ≈ 23 h 56 min 4 s ≈ 86 164 s et GMT ≈ 3,986.1014 m3s-2, il vient hg ≈ 35 786 km.
Finalement, on obtient a ≈ 24 371 km (≈ 3,82 RT), e ≈ 0,730 et b ≈ 16 654 km (≈ 2,61 RT)
Au passage, il est intéressant de noter que dans le Système solaire, le produit GM, que l’on appelle le paramètre gravitationnel standard, est généralement connu avec une précision supérieure à celle associée à chacun des deux facteurs G et M. La page suivante recense sa valeur pour le Soleil et les huit planètes du Système solaire :
https://en.wikipedia.org/wiki/Standard_gravitational_parameter