Durée du transfert géostationnaire

La durée du transfert vaut la moitié de la période d’un corps qui parcourrait la totalité de l’orbite elliptique.

Nous allons, pour calculer cette période, utiliser la 3^e loi de Kepler qui nous dit que dans notre problème, la quantité a³/T² est constante pour tous les objets en orbite autour d’un même corps céleste.

Si le couple (a,T) caractérise l’orbite circulaire géostationnaire et le couple (a’,T’) l’orbite de transfert elliptique, on a :

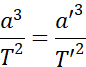
d’où

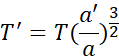
avec a’ = ½ (h_g + h_b + 2R_T), a = h_g + R_T et T ≈ 86 164 s. On obtient donc T ≈ 10 h 31 min.

La durée du transfert vaut la moitié de cette période, soit environ 5 h 16 min.